ادم در کودکان

توابع مثلثاتی زاویه ای. توابع مثلثاتی آرگومان عددی و زاویه ای. درس و ارائه با موضوع: "تابع مثلثاتی استدلال زاویه ای، اندازه گیری درجه زاویه و رادیان"

درس ویدیویی "توابع مثلثاتی یک استدلال زاویه ای" مواد بصری را برای اجرای یک درس ریاضی در موضوع مربوطه ارائه می دهد. این ویدئو به گونه ای طراحی شده است که مطالب مورد مطالعه تا حد امکان به راحتی برای دانش آموزان ارائه شود، به خاطر سپردن آسان باشد و ارتباط بین اطلاعات موجود در مورد توابع مثلثاتی از بخش مطالعه مثلث ها و تعریف آنها با استفاده از واحد را به خوبی نشان دهد. دایره. این می تواند به بخشی مستقل از درس تبدیل شود، زیرا به طور کامل این موضوع را پوشش می دهد و با نظرات مهم در طول صداگذاری تکمیل می شود.

برای نشان دادن واضح رابطه بین تعاریف مختلف توابع مثلثاتی، از جلوه های انیمیشن استفاده می شود. برجسته کردن متن با فونت رنگی، ساختارهای واضح و قابل فهم و اضافه کردن نظرات به شما کمک می کند تا به سرعت مطالب را به خوبی یاد بگیرید و به سرعت به اهداف درس برسید. ارتباط بین تعاریف توابع مثلثاتی به وضوح از طریق جلوه‌های انیمیشن و برجسته‌سازی رنگ نشان داده می‌شود و درک و حفظ مطالب را ارتقا می‌دهد. هدف این راهنما افزایش اثربخشی آموزش است.

درس با معرفی موضوع شروع می شود. سپس تعاریف سینوس، کسینوس، مماس و کوتانژانت یک زاویه حاد مثلث قائم الزاویه یادآوری می شود. تعریف برجسته شده در قاب به ما یادآوری می کند که سینوس و کسینوس به عنوان نسبت ساق به هیپوتنوز تشکیل می شوند، مماس و کوتانژانت از نسبت پاها تشکیل می شوند. همچنین مطالبی را که اخیراً آموخته اند به دانش آموزان یادآوری می شود که هنگام در نظر گرفتن نقطه ای روی دایره واحد، آبسیسا نقطه کسینوس و مختصات سینوس عدد مربوط به آن نقطه است. ارتباط بین این مفاهیم با استفاده از ساخت و ساز نشان داده شده است. صفحه نمایش یک دایره واحد را نشان می دهد که مرکز آن با مبدا منطبق است. از مبدأ مختصات، پرتویی ساخته می‌شود که با نیم محور آبسیسا مثبت زاویه α می‌سازد. این پرتو دایره واحد را در نقطه O قطع می کند. از نقطه، عمودهای عمود بر ابسیسا و محور مختصات پایین می آیند و نشان می دهند که مختصات این نقطه، کسینوس و سینوس زاویه α را تعیین می کند. لازم به ذکر است که طول قوس AO از نقطه تقاطع دایره واحد با جهت مثبت محور آبسیسا تا نقطه O همان قسمتی از کل قوس است که زاویه α از 360 درجه است. این به شما امکان می دهد نسبت α/360=t/2π را ایجاد کنید، که بلافاصله نمایش داده می شود و برای به خاطر سپردن با رنگ قرمز برجسته می شود. از این نسبت مقدار t=πα/180° به دست می آید. با در نظر گرفتن این موضوع، رابطه بین تعاریف سینوس و کسینوس مشخص می شود: sinα°= sint= sinπα/180، cosα°=cost=cosπα/180. به عنوان مثال، پیدا کردن sin60 درجه داده شده است. با جایگزینی درجه اندازه گیری زاویه به فرمول، sin π·60°/180° دریافت می کنیم. با کاهش 60 کسر، sin π/3 را بدست می آوریم که برابر با √3/2 است. توجه داشته باشید که اگر 60 درجه یک اندازه گیری درجه یک زاویه باشد، آنگاه π/3 اندازه گیری رادیانی یک زاویه نامیده می شود. دو نماد ممکن برای نسبت درجه یک زاویه به اندازه رادیان وجود دارد: 60°=π/3 و 60°=π/3 راد.

مفهوم زاویه یک درجه به عنوان زاویه مرکزی که توسط کمانی که طول آن 1/360 نشان دهنده بخشی از محیط است، تعریف می شود. تعریف زیر مفهوم زاویه یک رادیان را نشان می دهد - زاویه مرکزی بر اساس کمانی به طول یک یا برابر با شعاع دایره. تعاریف به عنوان مهم علامت گذاری می شوند و برای به خاطر سپردن برجسته می شوند.

برای تبدیل یک درجه یک زاویه به اندازه گیری رادیان و بالعکس، از فرمول α°=πα/180 راد استفاده کنید. این فرمول در یک قاب روی صفحه برجسته شده است. از این فرمول نتیجه می شود که 1° = π/180 راد. در این حالت، یک رادیان مربوط به زاویه 180°/π≈57.3 درجه است. خاطرنشان می شود که هنگام یافتن مقادیر توابع مثلثاتی متغیر مستقل t، می توان آن را هم یک آرگومان عددی و هم یک آرگومان زاویه ای در نظر گرفت.

در ادامه نمونه هایی از استفاده از دانش کسب شده در حل مسائل ریاضی را نشان می دهد. در مثال 1، شما باید مقادیر را از درجه به رادیان 135 درجه و 905 درجه تبدیل کنید. در سمت راست صفحه فرمولی وجود دارد که رابطه بین درجه و رادیان را نشان می دهد. پس از جایگزینی مقدار در فرمول، (π/180)·135 را بدست می آوریم. پس از کاهش 45 این کسر، مقدار 135° = 3π/4 را بدست می آوریم. برای تبدیل زاویه 905 درجه به اندازه گیری رادیانی از همین فرمول استفاده می شود. پس از جایگزینی مقدار در آن، معلوم می شود (π/180)·905=181π/36 راد.

در مثال دوم، مسئله معکوس حل شده است - اندازه گیری درجه زاویه بیان شده در رادیان π/12، -21π/20، 2.4π پیدا شده است. در سمت راست صفحه، فرمول مورد مطالعه را برای ارتباط بین درجه و اندازه گیری رادیان زاویه 1 rad = 180°/π به یاد می آوریم. هر مثال با جایگزین کردن اندازه گیری رادیان در فرمول حل می شود. با جایگزینی π/12، (180°/π)·(π/12)=15° دریافت می کنیم. مقادیر زوایای باقیمانده به طور مشابه -21π/20=-189 درجه و 2.4π=432 درجه یافت می شود.

درس تصویری "توابع مثلثاتی استدلال زاویه ای" برای استفاده در درس های ریاضی سنتی برای افزایش کارایی یادگیری توصیه می شود. این مطالب به اطمینان از دیده شدن یادگیری در طول آموزش از راه دور در این موضوع کمک می کند. توضیح دقیق و قابل فهم موضوع و راه حل های مشکلات مربوط به آن می تواند به دانش آموز کمک کند تا به طور مستقل بر مطالب تسلط یابد.

رمزگشایی متن:

"توابع مثلثاتی آرگومان زاویه ای."

ما قبلاً از هندسه می دانیم که سینوس (کسینوس) زاویه حاد مثلث قائم الزاویه نسبت ساق به هیپوتنوز و مماس (کتانژانت) نسبت پاها است. و در جبر ابسیسا یک نقطه روی دایره واحد را کسینوس و مختص این نقطه را سینوس می نامیم. بیایید مطمئن شویم که همه اینها از نزدیک به هم مرتبط هستند.

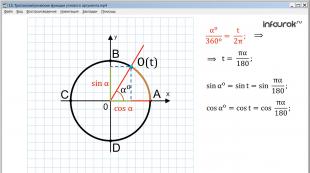
بیایید یک زاویه با اندازه درجه α° (درجه آلفا) قرار دهیم، همانطور که در شکل 1 نشان داده شده است: راس زاویه با مرکز دایره واحد (با مبدا سیستم مختصات) و یک طرف زاویه سازگار است. با پرتو مثبت محور آبسیسا سازگار است. ضلع دوم زاویه دایره را در نقطه O قطع می کند. مختص نقطه O سینوس زاویه آلفا و آبسیسا این نقطه کسینوس آلفا است.

توجه داشته باشید که قوس AO همان قسمتی از طول دایره واحد است که زاویه آلفا از زاویه سیصد و شصت درجه است. اجازه دهید طول قوس AO را با t(te) نشان دهیم، سپس نسبت = را بسازیم

(آلفا به شصت اعتماد است همانطور که te به دو پی است) از اینجا te را می یابیم: t = = (te برابر است با پی آلفا تقسیم بر صد و هشتاد).

بنابراین، برای پیدا کردن سینوس یا کسینوس زاویه آلفا درجه، می توانید از فرمول استفاده کنید:

sin α° = sint = sin (درجه سینوس آلفا برابر با سینوس ته و برابر با سینوس پی آلفا جزئی تا صد و هشتاد است)

cosα° = هزینه = cos (کسینوس درجه آلفا برابر کسینوس te و برابر است با کسینوس پی آلفا جزئی به صد و هشتاد).

برای مثال sin 60° = sin = sin = (سینوس شصت درجه برابر با سینوس پی در سه است، طبق جدول مقادیر پایه سینوس ها برابر است با ریشه سه در دو) .

اعتقاد بر این است که 60 درجه یک اندازه گیری درجه یک زاویه است، و (pi در سه) اندازه گیری رادیانی همان زاویه است، یعنی 60 درجه = خوشحالم(شصت درجه برابر است با پی ضربدر سه رادیان). برای اختصار، ما در مورد تعیین توافق کردیم خوشحالمحذف کنید، یعنی ورودی زیر قابل قبول است: 60 درجه = (نمایش اختصارات رادیان اندازه = راد.)

زاویه یک درجه، زاویه مرکزی است که قوسی را که (یک سیصد و شصتمین) قسمت کمان است، فرو می برد. زاویه یک رادیان، زاویه مرکزی است که روی کمانی به طول یک قرار دارد، یعنی کمانی که طول آن برابر با شعاع دایره است (زوایای مرکزی یک دایره را برای نشان دادن زاویه بر حسب رادیان پی در نظر می گیریم. روی دایره).

بیایید فرمول مهم برای تبدیل درجه به رادیان را به خاطر بسپاریم:

α° = خوشحالم. (آلفا برابر است با پی آلفا تقسیم بر صد و هشتاد، رادیان) به طور خاص، 1 درجه = خوشحالم(یک درجه برابر است با تقسیم بر صد و هشتاد رادیان).

از اینجا می توان دریافت که یک رادیان برابر است با نسبت صد و هشتاد درجه به پی و تقریباً برابر با پنجاه و هفت نقطه سه درجه است: 1 خوشحالم= ≈ 57.3 درجه.

از موارد بالا: وقتی در مورد هر تابع مثلثاتی صحبت می کنیم، به عنوان مثال در مورد تابع s = sint (es برابر است با sine te)، متغیر مستقل t(te) را می توان هم یک آرگومان عددی و هم یک آرگومان زاویه ای در نظر گرفت.

بیایید به نمونه هایی نگاه کنیم.

مثال 1. از درجه به رادیان تبدیل کنید: الف) 135 درجه. ب) 905 درجه.

راه حل. بیایید از فرمول تبدیل درجه به رادیان استفاده کنیم:

الف) 135 درجه = 1 درجه ∙ 135 = خوشحالم ∙ 135 = خوشحالم

(صد و سی و پنج درجه برابر است با پی ضربدر صد و هشتاد رادیان در صد و سی و پنج و پس از کاهش برابر است با سه پی ضربدر چهار رادیان)

ب) به همین ترتیب با استفاده از فرمول تبدیل اندازه گیری درجه به اندازه گیری رادیانی به دست می آوریم

905 درجه = خوشحالم ∙ 905 = خوشحالم

(نهصد و پنج درجه برابر با صد و هشتاد و یک پی سی و شش رادیان است).

مثال 2. بیان بر حسب درجه: الف) ; ب) - ج) 2.4π

(پی بیش از دوازده؛ منهای بیست و یک پی بیش از بیست؛ دو نقطه چهار پی).

راه حل. الف) بیایید عدد پی را دوازده درجه بیان کنیم، از فرمول تبدیل اندازه رادیان یک زاویه به درجه در 1 استفاده کنیم. خوشحالم=، دریافت می کنیم

خوشحالم = 1 خوشحالم∙ = ∙ = 15 درجه (پی ضربدر دوازده رادیان برابر است با حاصلضرب یک رادیان و پی ضربدر دوازده. به جای یک رادیان صد و هشتاد را به جای پی و کاهش، پانزده درجه می گیریم)

مشابه b) - = 1 خوشحالم∙ (-) = ∙ (-)= - 189 درجه (منهای بیست و یک پی ضربدر بیست برابر منهای یکصد و هشتاد و نه درجه)

ج) 2.4π = 1 خوشحالم∙ 2.4π = ∙ 2.4π = 432 درجه (دو نقطه چهار پی برابر است با چهارصد و سی و دو درجه).

توابع مثلثاتی آرگومان عددیما آن را مرتب کردیم نقطه A را روی دایره گرفتیم و به دنبال سینوس ها و کسینوس های زاویه β به دست آمدیم.

ما نقطه را به عنوان A تعیین می کنیم، اما در جبر اغلب به عنوان t تعیین می شود و تمام فرمول ها / توابع با آن آورده شده است. همچنین از قوانین منحرف نخواهیم شد. آن ها t - بنابراین این عدد مشخصی خواهد بود تابع عددی(مثلا sin t)

منطقی است که چون دایره ای با شعاع یک داریم، پس

توابع مثلثاتی آرگومان زاویهما همچنین با موفقیت آن را تجزیه و تحلیل کردیم - طبق قوانین، ما برای چنین توابعی خواهیم نوشت: sin α°، به این معنی که توسط α° هر زاویه با تعداد درجه هایی که نیاز داریم.

پرتو این زاویه نقطه دوم دایره (OA - نقطه A) و نقاط مربوطه C و B را برای تابع آرگومان عددی به ما می دهد، اگر به آن نیاز داشته باشیم: sin t = گناه α°

خطوط سینوس، کسینوس، مماس و کوتانژانت

هیچ وقت آن را فراموش نکن محور Y خط سینوس ها است, محور X خط کسینوس است! نقاط به دست آمده از دایره روی این محورها مشخص شده اند.

آ خطوط مماس و کتانژانت موازی آنها هستند و از نقاط (1; 0) و (0;1) عبور می کنند.به ترتیب.

هر عدد واقعی t را گرفته شود، می توان آن را با یک عدد sin t تعریف شده منحصر به فرد مرتبط کرد. درست است، قانون تطبیق بسیار پیچیده است؛ همانطور که در بالا دیدیم، به شرح زیر است.

برای پیدا کردن مقدار sin t با استفاده از عدد t، شما نیاز دارید:

1) دایره عددی را در صفحه مختصات قرار دهید تا مرکز دایره با مبدأ مختصات منطبق باشد و نقطه شروع A دایره در نقطه (1؛ 0) قرار گیرد.

2) نقطه ای از دایره مربوط به عدد t را پیدا کنید.

3) ترتیب این نقطه را بیابید.

این دستور گناه تی است.

در واقع، ما در مورد تابع u = sin t صحبت می کنیم که t هر عدد واقعی است.

همه این توابع نامیده می شوند توابع مثلثاتی آرگومان عددی t.

تعدادی رابطه وجود دارد که مقادیر توابع مثلثاتی مختلف را به هم متصل می کند؛ ما قبلاً برخی از این روابط را به دست آورده ایم:

sin 2 t+cos 2 t = 1

از دو فرمول آخر به راحتی می توان یک رابطه اتصال tg t و ctg t را بدست آورد:

همه این فرمول ها در مواردی استفاده می شود که با دانستن مقدار یک تابع مثلثاتی، لازم است مقادیر سایر توابع مثلثاتی محاسبه شود.

اصطلاحات "سینوس"، "کسینوس"، "مماس" و "کتانژانت" در واقع آشنا بودند، با این حال، آنها هنوز در تفسیر کمی متفاوت استفاده می شدند: در هندسه و فیزیک آنها سینوس، کسینوس، مماس و کتانژانت را در نظر می گرفتند. در سر(اما نه

اعداد، همانطور که در پاراگراف های قبلی بود).

از هندسه مشخص شده است که سینوس (کسینوس) یک زاویه تند نسبت پایه های یک مثلث قائم الزاویه به هیپوتنوز آن است و مماس (کتانژانت) یک زاویه، نسبت پایه های یک مثلث قائم الزاویه است. رویکرد متفاوتی به مفاهیم سینوس، کسینوس، مماس و کوتانژانت در پاراگراف‌های قبلی ارائه شد. در واقع این رویکردها به هم مرتبط هستند.

بیایید یک زاویه با درجه b o بگیریم و آن را در مدل «دایره عددی در یک سیستم مختصات مستطیلی» قرار دهیم، همانطور که در شکل نشان داده شده است. 14

راس زاویه با مرکز سازگار است

دایره ها (با مبدأ سیستم مختصات)،

و یک طرف زاویه با

پرتو مثبت محور x توقف کامل

تقاطع ضلع دوم زاویه با

با دایره حرف M را نشان دهید. Ordina-

شکل 14 b o و آبسیسا این نقطه کسینوس زاویه b o است.

برای یافتن سینوس یا کسینوس یک زاویه b o به هیچ وجه لازم نیست که این ساختارهای بسیار پیچیده را هر بار انجام دهید.

کافی است توجه داشته باشید که قوس AM همان قسمتی از طول دایره عددی را تشکیل می دهد که زاویه b o از گوشه 360 درجه ایجاد می کند. اگر طول کمان AM با حرف t نشان داده شود، به دست می آید:

بدین ترتیب،

مثلا،

اعتقاد بر این است که 30 درجه یک درجه یک زاویه است و اندازه گیری رادیانی همان زاویه: 30 درجه = راد. اصلا:

به ویژه، خوشحالم که به نوبه خود آن را از کجا دریافت می کنیم.

پس 1 رادیان چیست؟ اندازه گیری های مختلفی برای طول قطعات وجود دارد: سانتی متر، متر، یارد و غیره. همچنین معیارهای مختلفی برای نشان دادن بزرگی زاویه ها وجود دارد. زوایای مرکزی دایره واحد را در نظر می گیریم. زاویه 1 درجه، زاویه مرکزی است که توسط یک قوس که بخشی از یک دایره است، فرو رفته است. زاویه 1 رادیان، زاویه مرکزی است که توسط کمانی به طول 1 فرو رفته است، یعنی. روی کمانی که طول آن برابر با شعاع دایره است. از فرمول دریافتیم که 1 راد = 57.3 درجه است.

هنگام در نظر گرفتن تابع u = sin t (یا هر تابع مثلثاتی دیگر)، می‌توانیم متغیر مستقل t را یک آرگومان عددی در نظر بگیریم، همانطور که در پاراگراف‌های قبل انجام شد، اما می‌توانیم این متغیر را نیز معیاری برای اندازه گیری در نظر بگیریم. زاویه، یعنی استدلال گوشه بنابراین، هنگامی که در مورد یک تابع مثلثاتی صحبت می شود، به معنای خاصی تفاوتی ندارد که آن را تابعی از یک استدلال عددی یا زاویه ای در نظر بگیریم.

درس و ارائه با موضوع: "تابع مثلثاتی استدلال زاویه ای، اندازه گیری درجه زاویه و رادیان"

مواد اضافی
کاربران گرامی، نظرات، نقدها، خواسته های خود را فراموش نکنید. تمام مواد توسط یک برنامه ضد ویروس بررسی شده است.

دستورالعمل ها و شبیه سازها در فروشگاه آنلاین Integral برای درجه 10 از 1C
ما مسائل هندسه را حل می کنیم. وظایف ساختمان تعاملی
ما مسائل هندسه را حل می کنیم. وظایف تعاملی برای ساخت و ساز در فضا

آنچه ما مطالعه خواهیم کرد:
1. بیایید هندسه را به خاطر بسپاریم.
2. تعریف آرگومان زاویه ای.
3. درجه اندازه گیری زاویه.
4. اندازه گیری رادیانی زاویه.
5. رادیان چیست؟
6. مثال ها و وظایف برای حل مستقل.

تکرار هندسه

بچه ها، در توابع ما:

y= sin(t)، y= cos(t)، y= tg(t)، y= ctg(t)

متغیر t نه تنها می تواند مقادیر عددی را بگیرد، یعنی یک آرگومان عددی باشد، بلکه می تواند به عنوان معیار یک زاویه - یک آرگومان زاویه ای نیز در نظر گرفته شود.

بیایید هندسه را به یاد بیاوریم!
چگونه سینوس، کسینوس، مماس، کوتانژانت را در آنجا تعریف کردیم؟

سینوس زاویه - نسبت طرف مقابل به هیپوتنوز

کسینوس زاویه - نسبت پای مجاور به هیپوتنوز

مماس یک زاویه نسبت ضلع مقابل به ضلع مجاور است.

کتانژانت یک زاویه نسبت ضلع مجاور به ضلع مقابل است.

تعریف تابع مثلثاتی آرگومان زاویه

بیایید توابع مثلثاتی را به عنوان توابع آرگومان زاویه ای روی دایره عددی تعریف کنیم:
با استفاده از دایره اعداد و سیستم مختصات، همیشه می‌توانیم سینوس، کسینوس، مماس و کتانژانت یک زاویه را پیدا کنیم:

بیایید راس زاویه α خود را در مرکز دایره قرار دهیم، یعنی. به مرکز محور مختصات، و یکی از اضلاع را طوری قرار دهید که با جهت مثبت محور آبسیسا (OA) منطبق باشد.
سپس ضلع دوم دایره عددی را در نقطه M قطع می کند.

ترتیب دهیدنقطه M: سینوس زاویه α
اوکیسانقطه M: کسینوس زاویه α

توجه داشته باشید که طول قوس AM همان قسمت دایره واحد با زاویه α ما از 360 درجه است: جایی که t طول قوس AM است.

درجه اندازه گیری زاویه

1) بچه ها، ما فرمولی برای تعیین درجه یک زاویه از طریق طول قوس یک دایره عددی دریافت کردیم، بیایید نگاهی دقیق تر به آن بیندازیم:

سپس توابع مثلثاتی را به شکل زیر می نویسیم:

مثلا:

اندازه گیری رادیانی زاویه ها

هنگام محاسبه درجه یا اندازه گیری رادیان یک زاویه، به یاد داشته باشید! :
مثلا:

راستی! راد تعیین. می توانید آن را پایین بیاورید!

رادیان چیست؟

دوستان عزیز، ما با یک مفهوم جدید روبرو هستیم - رادیان. پس چیست؟

اندازه گیری های مختلفی از طول، زمان، وزن وجود دارد، به عنوان مثال: متر، کیلومتر، ثانیه، ساعت، گرم، کیلوگرم و غیره. پس رادیان یکی از معیارهای زاویه است. ارزش در نظر گرفتن زوایای مرکزی، یعنی آنهایی که در مرکز دایره اعداد قرار دارند، می باشد.
زاویه 1 درجه، زاویه مرکزی است که توسط قوسی برابر با 1/360 محیط فرو رفته است.

زاویه 1 رادیان، زاویه مرکزی است که توسط یک قوس برابر با 1 در یک دایره واحد، و در یک دایره دلخواه توسط یک قوس برابر با شعاع دایره فرو رفته است.

مثال ها: